コンピューターにおいて小数値を表現する形式について解説します。
Contents
コンピューターで小数値を表す形式は、大きく2つある
小数点を含む小数値をコンピューターで表す形式には、「固定小数点形式」と「浮動小数点形式」があります。
○固定小数点形式
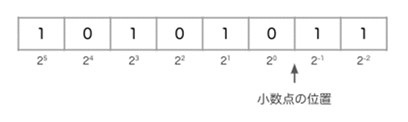
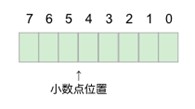
小数点の位置を固定して表す形式です。例えば以下の例では、8ビットのデータ列の下から2桁目と3桁目の間を小数点の位置としています。
ただし固定小数点形式においては、小数点の位置を最後の位置に固定し、整数(-2、-1…0、1、2などの数で、小数や分数は含まない。)のみ取り扱う方法が、一般的に用いられています。
また固定小数点形式には、正の値のみを表す「符号なし」と、正負の値を表す「符号付き」の形式があります。
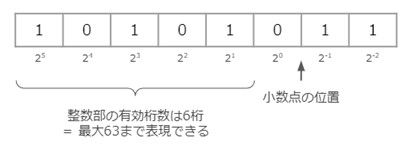
符号なしの場合、正の値しか表現することができません。しかし符号付きと比べた場合、有効桁数が1ビット分増えるため、表現できる数の範囲は広くなります。
反対に号付きの場合、先頭のビットを正負を表す符号(符号ビット)として利用するため、符号なしに比べると表現できる数の範囲は狭くなります。
※符号ビットは0が正の数、1が負の数を表します。
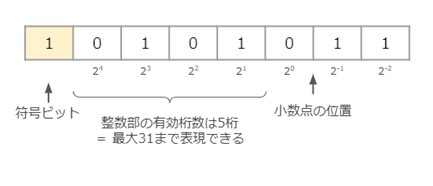
固定小数点の「符号なし」と「符号あり」どちらの表現形式を使うかは、負の値を取り扱うかどうかで決めると良いでしょう。
8ビット、16ビットの固定小数点数で表せる整数の範囲は、次のようになります。
| ビット数 | 符号 | 最小/最大 | 小数点の位置 | 2進数 | 10進数 |
|---|---|---|---|---|---|
| 8ビット | なし | 最小値 | 任意(どの位置でも0になるため) | 00000000 | 0 |
| 8ビット | なし | 最大値 | 最下位ビットの右側 | 11111111 | 255 |
| 8ビット | あり | 最小値 | 最下位ビットの右側 | 10000000 | -128 |
| 8ビット | あり | 最大値 | 最下位ビットの右側 | 01111111 | 127 |
| 16ビット | なし | 最小値 | 任意(どの位置でも0になるため) | 0000000000000000 | 0 |
| 16ビット | なし | 最大値 | 最下位ビットの右側 | 1111111111111111 | 65535 |
| 16ビット | あり | 最小値 | 最下位ビットの右側 | 1000000000000000 | -32768 |
| 16ビット | あり | 最大値 | 最下位ビットの右側 | 0111111111111111 | 32767 |
固定小数点形式は、浮動小数点形式と比べると、以下のような特徴があります。
- 表現できる値の範囲が狭い
- 整数値の計算と同じように処理できることから、高速に演算できる
(整数値か少数値かに関わらず、仮数・指数・基数で構成されている数字を展開して計算する必要があるため固定小数点形式の方が計算が速くなります。)
○浮動小数点形式
小数点の位置を固定せずに表す形式です。数を「符号部」「指数部」「仮数部」の3つに分けて、それぞれの部を「0」と「1」だけで表現することでマイナス符号や小数点の位置を決め、非常に小さな数から大きな数まで、より広範囲の値を効率的に表現します。
浮動小数点数が考えられた背景として、科学技術計算のように天文学的な数字をコンピューターで扱うために、より広い範囲の値を効率的に表現する仕組みが必要だったことが挙げられます。
例えば「0.00000000011253」「230000000000111」のような値を固定小数点数で表そうとすると、数値の多くは0ですが、非常に多くの桁数(ビット数)が必要になります。8ビットでは桁数が足りず表現しきれません。
しかし浮動小数点数では、こうした桁数の大きな値でも、限られたビット数で表現することができます。
浮動小数点数は、基本的に以下の形式を取ります。
- 指数表記を用いる
- ビット列を左から「符号部 | 指数部 | 仮数部」に分けて表す
- 使用するビット数に応じて「単精度(32ビット)」「倍精度(64ビット)」などいくつかの形式がある
- 単精度(32ビット):符号部1ビット・指数部8ビット・仮数部23ビット
- 倍精度(64ビット):符号部1ビット・指数部11ビット・仮数部52ビット
指数表記とは、非常に大きな数や小さな数を表現するときに使用される表記方法です。
± m×Re
mは仮数部、Rは基数、eは指数部と呼びます。
仮数(m)を0.00025、基数(R)を10とした場合、0.00025 = 0.25×10-3というように表現することができます。
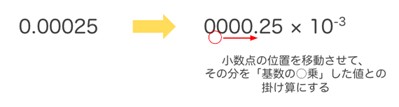

コンピューターでは2進数を扱うため、指数表記における基数は必ず「2」になりまです。固定部分を記憶しておく必要はないので、残りの可変部分(符号部・指数部・仮数部)の値を各ビットに割り当てて、数を表現します。
また浮動小数点数の仮数部には「正規化」した値が入ります。正規化とは、小数点の位置を調節することで、その後の計算で発生する誤差を減らすための処理です。そのため仮数の最上位桁が必ず0(ゼロ)以外の数値になるように調整します。
例えば「0.123×10-3」と「0.0123×10-2」は小数点の取り方が違うだけで、数値としては全く同じです。
仮数部を3桁の入れ物に保管すると考えた場合、元の値をきちんと保持できるのは「0.123×10-3」の方になります。
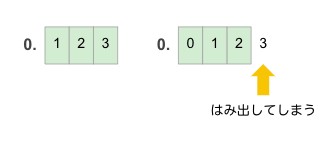
このように、ある数を表すときの仮数部と指数部の値の取り方には色々なパターンがありますが、正規化することで、限られたビット数の中でなるべく多くの桁数(有効桁数)を持てるようになり、誤差が減りより正確な計算ができるようになります。
次に、32ビットの単精度浮動小数点数を例に、もう少し詳しく見ていきます。

| 符号部 | 仮数部の符号を表す部分で「0:正」か「1:負」のいずれかを示します。 |
| 指数部 | 負の数は2の補数で表現します。 |
| 仮数部 | 2進数の絶対値表示です。小数部の最上位桁が0にならないよう「0.M」の形式に正規化したときの、Mの値が入ります。 |
上記の形式を用いて、10進数の0.1875という数字を表現してみます。
①10進数から2進数に変換する
10進数の0.1875を2進数に変換すると、0.0011になります。
②2進数を正規化する
小数部の最上位桁が0以外の値になるように、①で求めた2進数を正規化します。
0.0011 → 0.11 × 2-2
③符号部・仮数部・指数部の値を抜き出す
| 符号部 | 正の数なので「0」 |
| 指数部 | 11(0.Mの形式に正規化した時のMの値) |
| 仮数部 | 指数を7ビットの2進数で表します。10進数の「-2」は、2進数の「0000010」の2の補数で「1111110」となります。 |
④抜き出した値を指定された形式に当て込む
10進数の0.1875を32ビットの浮動小数点数で表現すると次のようになります。仮数部は24ビットあるため、3桁目以降は0で埋めます。

上記の他にも、浮動小数点数にはいくつかの表現形式があります。
○IEEE 754による単精度浮動小数点数、倍精度浮動小数点数
最も広く採用されているのは「IEEE 754」という国際的な標準規格で、「単精度浮動小数点数」と「倍精度浮動小数点数」の2種類があります。
○単精度浮動小数点数
符号部・指数部・仮数部を1ビット・8ビット・23ビットとして表現する
全体32ビット
○倍精度浮動小数点数
符号部・指数部・仮数部を1ビット・11ビット・52ビットとして表現する
全体64ビット
IEEE 754は、一般的なコンピューターのCPUでも採用されていますが、処理において単精度・倍精度のどちらを使うかはCPUの判断になるため、私たちがコンピューターを使うときに使い分けを意識する必要はありません。
なお、規格名の先頭にある「IEEE」は米国電気電子学会の略称で、電気やコンピューターにおける技術の標準化を推進している団体です。
下の図は、10進数の45.625を、IEEE 754形式の単精度浮動小数点で表したものです。

10進数の小数を2進数の浮動小数点に変換する流れは、以下のとおりです。
①10進数から2進数に変換する
45.625 → 101101.101
②整数部分が1となるように、小数点の位置をずらす(この手順を「けち表現」と呼びます)
101101.101 → 1.01101101
※けち表現・・・正規化後の仮数部の最上位桁は必ず「1」になるため、この1が常に1の位に来るようにシフトして、そのときの小数点以下を23ビットで表す形式です。仮数の整数部分は「1」しかないため、メモリ中で「1」は記録しなくてもよいことになり、1ビットだけメモリを節約できます。
この状態から、仮数部と指数部の値をそれぞれ求めていきます。
○符号部
正の値であれば0、負の値であれば1が入ります。
○仮数部
②の小数点の右側部分(01101101)が仮数部となります。単精度浮動小数点数の場合、仮数部は23ビットですので、足りない分は後ろを0で埋めます。
01101101000000000000000

なお、仮数部は23ビットや64ビットで示されるため、極端に大きな値や小さな値は、近似値でしか表すことができません。
○指数部
②の時に小数点をずらした数が、指数部の値になります。今回は左方向に5桁ずらしているため指数部は「5」ですが、IEEE 754で表現する場合は、さらに127を加えてバイアスをかける(※)必要があります。
5 + 127 = 132 → 2進数に変換して 10000100
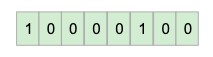
※ バイアスには「下駄を履かせる」という意味があります。127を加えることで、次の表のように負の数を含む表現が正の数だけで表せるため、浮動小数点数の大小関係が分かりやすくなります(人の目から見た大小関係は関係なく、コンピューターが効率的に計算するための考え方です。バイアスをかけない場合、コンピューターは指数部と仮数部をそれぞれ考慮する必要が出てくるため、整数用の比較演算では大小が判定できず、浮動小数点専用の比較演算が必要になってしまいます。)。効率的に演算するために考えられたルールである、と覚えておきましょう。
| 実際の指数 | バイアス | バイアスをかけた後の指数 | 2進数 |
| -127 | 127 | 0 | 00000000 |
| 0 | 127 | 127 | 01111111 |
| 128 | 127 | 255 | 11111111 |
IEEE754の指数部では2の補数は使いませんので、指数部は8ビットあるので、符号なし整数と見なす場合は「0〜255」までの値が使えますが、0と255は特別な値としてコンピューターで予約されているので使えません。
表せる範囲が1~254となるので、下記の考え方から、負数も表現するために255の中央値である127(端数切り捨て)をバイアス値にしたと考えられています。指数部の最小値は 1-127 = -126 (127足すと1になる)
指数部の最大値は 254-127 = 127(127足すと254になる)
IEEE754の指数部では2の補数は使いませんので、普通に考えると0~255の範囲となります。
0と255は特別な値としてコンピューターで予約されているので使えません。
そのため表せる範囲が1~254となるので、下記の考え方から、IEEE754の指数部の範囲は「-126~127」となります。
情報処理技術者試験の過去問題に挑戦してみよう
固定小数点数・浮動小数点数は、情報処理技術者試験の午前問題で出題されることがあります。以下は平成22年春期試験で実際に出された問題です。
実際に解けるか、ぜひ挑戦してみてください。(下に解説があります)
①浮動小数点数
以下は平成22年春期試験で実際に出された問題です。
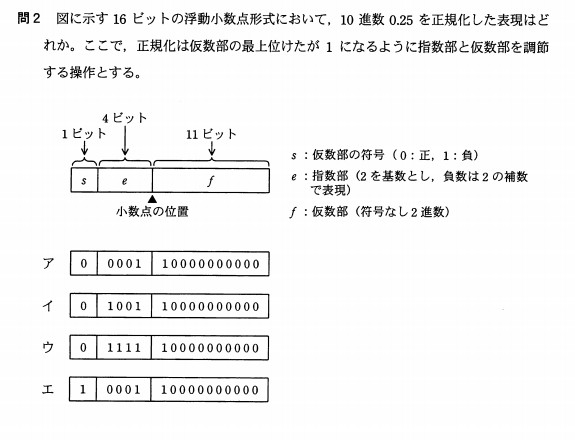
正解:ウ
①10進数の0.25を2進数に変換する
0.25 → 0.01
②仮数部の最上位けたが1になるように正規化する
0.01 → 0.1(0.01 × 2-1)
③符号、指数部、仮数部をそれぞれ求める
符号:正の値のため0
指数部:小数点を右に1つずらしたので、指数部は「-1」となる。問題文には「負数は2の補数で表現」とあるので、負数「-1」を2の補数に変換。
10進数の「1」を2進数に変換すると、「0001」。各桁を反対にし、「1」を加算。
0001 → 1110 → 1111
仮数部:最上位桁が1で全体11ビットのため、10000000000
②固定小数点数
以下は平成23年秋期試験で実際に出された問題です。
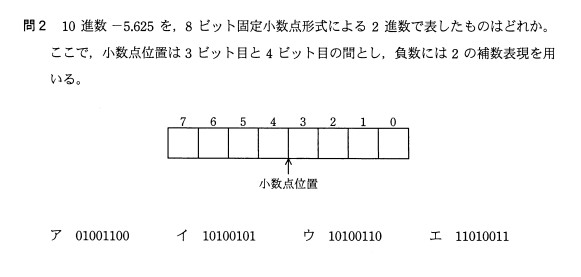
正解:ウ
①正数の5.625を2進数にする
0101.1010
②2の補数で表現する
0101.1010 → ビット反転(1010.0101) → 1を加算(1010.0110)
※2の補数は、各ビットを反転させた後、小数部も含めた最下位ビットに対して1を加算します。
演習問題
【問題1】10進数を固定小数点数形式の2進数で表そう
10進数の-0.1875を、8ビット固定小数点形式による2進数に変換してください。小数点位置は、4ビット目と5ビット目の間とし、負数は2の補数表現を利用します。
○解答
001.11010
○解説
次の手順で変換します。
①10進数の0.1875を2進数に変換する
0.0011
②2の補数表現を用いてマイナスに変換する
0.0011 → ビット反転して 1.1100 → 最下位ビットに1加算して 1.1101
③8ビットで表現する
以下の枠に②の結果を当てはめると「001.11010」となる
【問題2】色々な基数で浮動小数点数を表現しよう
次の形式の浮動小数点数で、10進数の50を、基数を2とした場合・基数を16とした場合それぞれで表現してください。

○解答
基数を2とした場合:0 0000110 110010000000000000000000
基数を16とした場合:0 0000010 001100100000000000000000
○解説
符号部をS、指数部をE、仮数部をM、基数をBとする。
基数を2とした場合:
①10進数の50を M×BEの形式に変換する
10進数の50 → 2進数の00110010 → 00110010 × 20
②仮数部の値が 1/2 ≦ M < 1 の範囲に入っていない場合は正規化を行う
00110010 × 20 → 0.11001 × 26
③32ビットで表現する
問題冒頭の枠に②を当てはめると「0 0000110 110010000000000000000000」となる
基数を16とした場合:
①10進数の50を M×BE の形式に変換する
10進数の50 → 16進数の32 → 32 × 160
②仮数部の値が 1/16 ≦ M < 1 の範囲に入っていない場合は正規化を行う
32 × 160 → 0.32 × 162
③仮数部を2進数に変換する
基数が16であっても、最終的には「0」か「1」のビット列で表現するため、2進数の値へと変換する必要があります。16進数から2進数への変換は、変換する値の各桁を4桁の2進数に変換することで簡単に求められます。
②で正規化した仮数部は「32」→ 3と2をそれぞれ2進数にすると「0011」「0010」
④32ビットで表現する
問題冒頭の枠に②③を当てはめると「00000010001100100000000000000000」となる
【問題3】あるビット数での浮動小数点数の最大値を求めよう
次の25ビットの浮動小数点形式で表現できる最大値を表すビット列を、16進数として表すと、どのような値になるでしょうか。
符号部:仮数部の符号(0は非負、1は負)
指数部:実際の指数に64を加算したもの(0≦指数部≦127)
仮数部:絶対値表現
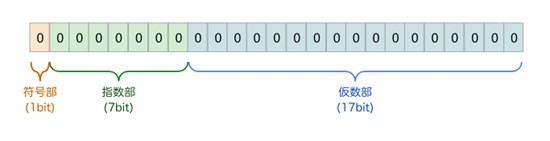
ここで、符号部をS・指数部をE・仮数部をMとした場合、この形式で表現される値は(-1)S × 16E-64 × 0.Mとします。
(符号部が-1のS乗で表されるのは、-1の0乗=1、-1の1乗=-1のため。)
(指数部でEから64をマイナスしていますが、64は負の指数を表すためのバイアス値です。
7ビットの場合、通常は0〜127までしか表現できませんが、バイアスによって-64〜63の値を表現しています。)
参考:https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1353751363
○解答
FFFFFF
○解説
| ①符号部 | 浮動小数点形式の表現において最大値を求める場合、先頭の1ビットは仮数部の符号であり、正の数>負の数なので、非負を表す0となります。 |
| ②指数部 | 0以上127以下なので、その範囲内で最大値である127を2進数で表現した「1111111」を設定します。 |
| ③仮数部 | 絶対値が最も大きくなるようにするため、17ビットすべてを1とした「11111111111111111」を設定します。 |
①②③を指定された形式に合わせると「0111111111111111111111111」となり、これを16進数に変換すると「FFFFFF」になります。
【問題4】あるビット数での固定小数点数の最小値を求めよう
負数を2の補数で表す16ビットの符号付き固定小数点数の最小値を表すビット列を、16進数として表すと、どのような値になるでしょうか。
○解答
8000
○解説
固定小数点数で負数を表現する場合、最上位ビットを符号ビットとした2の補数表現が用いられます。nビットで表現できる値の範囲は「-2n-1~2n-1-1」となっており、これにn=16を当てはめた場合、16ビットの符号付き固定小数点数では-32768〜32767の範囲を表現することができます(2の8乗×2の8乗 = 256×256など、工夫して計算すると求めやすいです)。
最初値である-32768の絶対値を2進数で表現すると「1000000000000000」(※)なので、これを2の補数を使い負数として表現します。
※32768 = 2の15乗であることが分かれば、10進数から2進数への変換は、桁の重みを使うと比較的簡単に変換可能です。
例)8 = 2の3乗 = 2の3乗×1 + 2の2乗×0 + 2の1乗×0 + 2の0乗×0 = 1000)。
1000000000000000
↓ ビットを反転させる
0111111111111111
↓ 1を加算する
1000000000000000
↓ 16進数に変換する
8000
