「N進法(進数)」の基本的な考え方について説明します。
とっつきにくい内容ですが、一度ルールさえ覚えてしまえば、決して難しいものではありません。
小数の基数変換も紹介します。
例題、練習問題も解きながら理解を深めてください。
Contents
N進法とは?
N進法とは数を表現するための方法のひとつで、「位取り記数法」とも呼ばれます。
N進法の「N」は、使用できる数字・記号の種類の数を表します。
例えば2進法であれば「0」と「1」の2二種類、8進法であれば「0」~「7」の8種類、12進法であれば0〜9の10種類の数字と3種類のアルファベット、16進法であれば0〜9およびA〜Fの10種類の数字と6種類のアルファベットを使うことができます。
N進数
まずは、10進法を例に見ていきます。
10進法では、以下のルールで数を表現します。
・数を数えるときは0~9の10種類の数字を使い、10になると桁がひとつ繰り上がる
10進法の数は 0 → 1 → 2 → 3 … → 9 と進んでいき、10種類の数字をすべて使い切ったところで桁がひと桁繰り上がって10となります。
このような桁の繰り上がり方は、10進法を含むすべてのN進法において、数の進み方の基本となる考え方です。
実は10進法の他にもうひとつ、私たちの日常でよく使われているN進法があります。
「時計」の60進法です。
一般的な時計が表す時間の最小単位は「秒」で、1秒、2秒…と時間が進んでいき、60秒になると「分」へ単位が繰り上がります。
同じように「分」から「時間」への繰り上がりも60分です。
つまり時計は「60進法」であると考えることができるのです。
人間が直感的に分かりやすい10進法以外に、なぜ様々なN進法があるのか、不思議に思った方もいるかもしれません。
もともとN進法は、大きな単位の数を処理しやすくするために、はるか昔インドで発明された考え方です。もしN進法がなければ、数を数えるときに 0、1、2…9、○、▲、☆… というような形で膨大な種類の数字・記号を用意する必要が出てきます。
そこでN進法の基本となる「位」の考え方により、数のまとまりを作り、そのまとまりの数を数えるようにすることで、0〜9の限られた数字だけで大きな単位の数を表すようにしました。
例えば 555 という数の場合、一の位・十の位・百の位で同じ数字が使われていますが、百の位は「100のまとまりが5つ」、十の位は「10のまとまりが5つ」、一の位は「1のまとまりが5つ」と、それぞれの数字が表現する数の大きさは違います。
これは位によって、数の基本的な大きさ(『重み』と表現します)が違うためです。
| 位 | 百の位 | 十の位 | 一の位 |
|---|---|---|---|
| 重み | 100倍 | 10倍 | 1倍 |
重みの増え方には規則性があり、10進法の場合、位が一つ上がるごとに10倍されていきます。
この重みの考え方を数式で表すと、以下のようになります。
555 = (100 × 5) + (10 × 5) + (1 × 5) = (102 × 5) + (101 × 5) + (100 × 5)
10進法の各位の重みは、位が上がるごとに10倍されていくため、イコールの一番右側の式のように、10のべき乗で表現することができます。
この、べき乗される数を「基数」と呼び、10進法の基数は10です。また、100の0や102の2のように、べき乗する回数を「指数」といいます。
| 位 | 百の位 | 十の位 | 一の位 |
|---|---|---|---|
| 数値 | 5 | 5 | 5 |
| 重み | 102(100) | 101(10) | 100(1) |
| 各桁の値 | 500 | 50 | 5 |
小数点以下についても見ていきます。
以下の表のとおり、小数点以下が増えるたびに重みは1/10倍されていきます。
| 位 | 一の位 | 小数点第一位 | 小数点第二位 |
|---|---|---|---|
| 重み | 1倍 | 0.1倍 | 0.01倍 |
5.55 という数を例に数式で表してみると、以下のようになります。
5.55 = (1 × 5) + (0.1 × 5) + (0.01 × 5)
= (1 × 5) + (1/10 × 5) + (1/100 × 5)
= (100 × 5) + (10-1 × 5) + (10-2 × 5)
小数をべき乗で表現する場合、指数はマイナス(指数がプラスの場合は掛け算・マイナスの場合は割り算と考えてください)となります。1/10 であれば、10-1と表現されます。
| 位 | 一の位 | 小数点第一位 | 小数点第二位 |
|---|---|---|---|
| 数値 | 5 | 5 | 5 |
| 重み | 100(1) | 10-1(0.1) | 10-2(0.01) |
| 各桁の値 | 5 | 0.5 | 0.05 |
この基数と指数の考え方は、あらゆるN進法に応用できますので、重要なキーワードとして抑えておいてください。2進法であれば基数が2、8進法であれば基数が8に変わるだけで、べき乗(指数)の考え方は10進法と全く同じです。
○コラム:どのN進法を採用する?
数を数えるときにどのN進法を採用するかは、様々な理由から決められてきました。時計のように自然界の法則に合わせて決められたものもあれば、鉛筆の販売単位としても使われている「ダース」のように、モノを分けやすいという理由で12進法(12 = 2・3・4・6 と色々な分け方ができる)を採用しているものもあります。
※1ダース=12である由来は諸説ありますが「分けやすいから」が有力な説です。
なお、コンピューターの世界においては、現在では2進法が基本となっています。
コンピューターが2進法を利用している主な理由は、0と1の2種類の値で全て(文字や数字や画像などのデータ、計算などの命令処理)を表現できるという点が、コンピューターが数字を扱う上で都合が良かったためです。
コンピューターをはじめとするデジタル機器は、入力されたデータを電気信号に変換し、その信号の大きさ(正確には電圧の強さ)によって入力値を判別しています。しかし電気信号はノイズ(雑音)などによって不安定になることが多く、10進法で入力を解釈しようとした場合、コンピューターが誤って判断してしまう可能性が大変高くなります。
2進法であれば「電気が流れているときは1」「電気が流れていないときは0」という判断で対応できるため、信号のノイズの影響を受けにくくなります。また10進法の場合よりも回路がシンプルになり、より簡単かつ高速に処理を行なうことができます。
2進法の表し方
コンピューター内部の世界で使われている2進法について説明します。先ほどの10進法と同じように2進法のルールをまとめると、以下のようになります。
・数を数えるときは0と1の数字を使い、2になると桁がひとつ繰り上がる
次の表は、10進法の0〜5までを2進法で表したものです。
| 10進法 | 2進法 | 説明 |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | |
| 2 | 10 | 2桁目に繰り上がる |
| 3 | 11 | |
| 4 | 100 | 3桁目に繰り上がる |
| 5 | 101 |
0と1で複数の値を表現することへのイメージを深めるために、表と裏のあるコインを例に考えてみましょう。コイン1枚では、表と裏の2通りの状態を表すことができます。

コインが2枚に増えると「表表」「表裏」「裏表」「裏裏」の4通りを表せます。これは、1枚目の状態が2通り、2枚目の状態が2通りの組み合わせになるため、2×2=4通りというように計算することもできます。同じように考えると、コイン3枚では2×2×2=23=8通り、コイン4枚では2×2×2×2=24=16通り…となり、コインn枚に対して2n通りの状態を区別できることが分かるかと思います。
それでは、カレンダーの日付(1日〜31日)をコインで表すには、何枚のコインが必要になるでしょうか。25=32ですので、5枚のコインがあれば十分そうです。
このとき、例えば「1枚だけ表なら1日」というのはイメージしやすいと思いますが、20日や31日を表すには、どのように考えれば良いでしょうか。
考え方の一つとして、5枚あるコインのそれぞれに、1・2・4・8・16の数字を与えて重み付けをすることで、1〜31の数字が表現できます。

この重み付けの考え方は、次に説明する「基数変換」の理解に非常に役立ちますので、ぜひ覚えておいてください。
基数変換
N進法の数を、別のN進法の数に変換することを「基数変換」と呼びます。
最初に、出題頻度の高いN進法と10進法同士の基数変換について見ていきます。
・N進数から10進数への変換
整数部と少数部に分けて説明します。
○整数部のN進数から10進数への変換
N進法の数を10進法で表すには、以下の手順で変換します。
①N進法の数の各桁の値に、その桁の「重み」を掛ける
②各桁の①の結果を足し算する
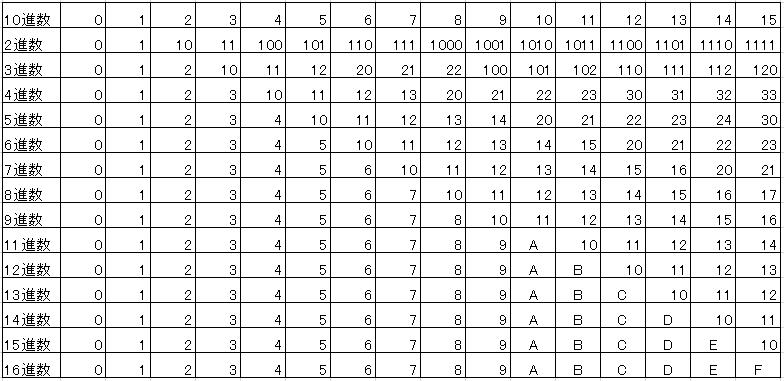
例として、2進法の「1011001」を10進法の数に変換してみましょう。
①N進法の数の各桁の値に、その桁の「重み」を掛ける
2進法の場合、基数が2となるため、各桁の重みは1桁目から 20、21、22…です。
図にすると以下のようなイメージです。
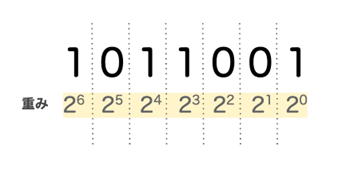
それぞれの桁に重みを掛けると、以下の計算結果となります。
7桁目・・・1 × 26 = 64
6桁目・・・0 × 25 = 0
5桁目・・・1 × 24 = 16
4桁目・・・1 × 23 = 8
3桁目・・・0 × 22 = 0
2桁目・・・0 × 21 = 0
1桁目・・・1 × 20 = 1
②各桁の①の結果を足し算する
あとは単純に、①で計算した結果を足し算していきます。
64 + 0 + 16 + 8 + 0 + 0 + 1 = 89
この計算結果より、2進法の「1011001」は、10進法に変換すると「89」となります。
2進法以外のN進法でも、①の基数が変わるだけで、手順としては全く同じです。
8進法「234」を10進法の数に変換する場合は、(2 × 82) + (3 × 81) + (4 × 80) = 128 + 24 + 4 = 156 となります。
なお、このときに重みを掛けられる側の数がアルファベットの場合は、10進法に換算して計算します。
例えば16進法のAであれば11、Fであれば15といった具合です。
16進法の「1F7」を10進法の数に変換する場合は、(1 × 162) + (15 × 161) + (7 × 160) = 256 + 240 + 7 = 503 となります。
○小数部のN進数から10進数への変換
次に、小数の場合の変換について説明します。
手順は整数の場合と基本的に同じ
①N進法の数の各桁の値に、その桁の「重み」を掛ける
②各桁の①の結果を足し算する
ですが、各桁に掛ける重みが異なってきます。
例として、2進法の「0.01011」を10進法の数に変換してみましょう。
①N進法の数の各桁の値に、その桁の「重み」を掛ける
整数の場合は、桁が大きくなるごとに重みが 20、21、22… と変化していきました。小数の場合は、桁が大きくなるごとに 2-1、2-2… と変化します。
図にすると以下のようなイメージです。
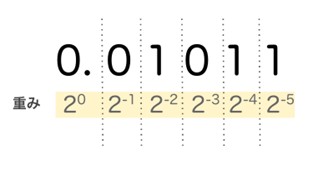
負の指数については高校数学で取り扱われますが、以下の式で表されます。つまり2-1は1/2と等しく、2-2は1/4と等しい、ということになります。
上記を踏まえてそれぞれの桁に重みを掛けると、以下の計算結果となります。
1桁目・・・0 ×20 = 0
小数点以下1桁目・・・0 × 2-1 = 0
小数点以下2桁目・・・1 × 2-2 = 1/4 = 0.25
小数点以下3桁目・・・0 × 2-3 = 0
小数点以下4桁目・・・1 × 2-4 = 1/16 = 0.0625
小数点以下5桁目・・・1 × 2-5 = 1/32 = 0.03125
②各桁の①の結果を足し算する
あとは単純に、①で計算した結果を足し算していきます。
0 + 0 + 0.25 + 0 + 0.0625 + 0.03125 = 0.34375
この計算結果より、2進法の「0.01011」は、10進法に変換すると「0.34375」となります。
・10進数からN進数への変換
整数部と少数部に分けて説明します。
○整数部の10進数からN進数への変換
10進法の数をN進法で表すには、2通りの方法があります。
方法1:割り算を使う
①10進法の数をNで割っていき、余りを計算する
②①の結果を下から上に順に並べていく
方法2:重み表を使う
①N進法の重みを計算した重み表を作る
②引くことができる一番大きい重みを引いていく
一般的には方法1で変換しますが、どちらでも同じ結果が得られますので、自分がやりやすい方法を選択してください。
方法1:割り算を使う
まず方法1の手順で、先ほどの例で使った10進法の「89」を、2進法の数に変換してみます。
①10進法の数をNで割っていき、余りを計算する
89を2で割っていき、商が0になる(これ以上2で割れなくなる)まで、どんどん余りを求めていきます。
図にすると以下のようなイメージです。
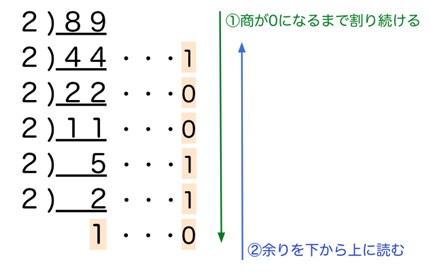
②①の結果を下から上に順に並べていく
2で割っていった余りを下から並べていきます。
1 0 1 1 0 0 1
この計算結果より、10進法の「89」は、2進法に変換すると「1011001」となります。先ほどの2進法→10進法の計算とも辻褄が合います。
同じ手順で10進法の「503」を16進法に変換してみます。503を16で割っていき、割り切れなくなるまで余りを求めます。
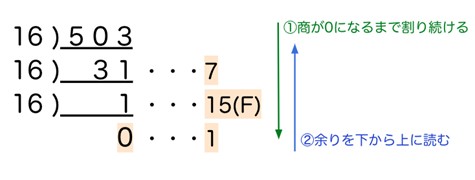
余りを下から並べるときには、16進法の数への変換を忘れないようにしましょう。10〜15の余りが出た場合はA〜Fのアルファベットに置き換えます。
この計算結果より、10進法の「503」を16進法の「1F7」に変換することができました。
最後に、方法1の手順②で、余りを下から並べる理由について説明します。
例えば5進法の数abcを、重みを掛けて10進法の数に変換すると、a × 52 + b × 51 + c × 50です。この10進法の数を、5で割ってみましょう。
(a × 52 + b × 51 + c × 50)÷ 5 = a × 51 + b × 50 余り c
(a × 51 + b × 50)÷ 5 = a × 50 余り b
a ÷ 5 = 0 余り a
5で割っていった場合、このように小さい桁の数字から余りになるため(c→b→a)、下から書き並べる(abc)のです。
方法2:重み表を使う
次に方法2の手順で、10進法の「89」を2進法の数に変換してみましょう。
①N進法の重みを計算した重み表を作る
2進法で重みを計算した表を作ります。
| 重み | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|
| 計算した重み | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 2進法の数 |
②引くことができる一番大きい重みを引いていく
②-① 89 < 128 なので、64の重みの欄に 64 × □ <= 89 となる「1」を書く。
| 重み | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|
| 計算した重み | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 2進法の数 | 1 |
②-② 残りは89 – 64 = 25。25 < 32 なので、32の重みの欄には「0」を書く。
次に大きい16の重みの欄に 16 × □ <= 25 となる「1」を書く。
| 重み | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|
| 計算した重み | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 2進法の数 | 1 | 0 | 1 |
②-③ 残りは25 – 16 = 9。8の重みの欄に 8 × □ <= 9 となる「1」を書く。
| 重み | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|
| 計算した重み | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 2進法の数 | 1 | 0 | 1 | 1 |
②-④ 残りは1。4の重みの欄と2の重みの欄には「0」、1の重みの欄に「1」を書く。
| 重み | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
|---|---|---|---|---|---|---|---|---|
| 計算した重み | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 2進法の数 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
10進法の89を2進法に変換すると「1011001」という正しい結果が得られました。8進法や16進法など他のN進法においても、重みの部分を変えるだけで、同じように10進法からの基数変換を行なうことができます。
○小数部の10進数からN進数への変換
小数点以下の場合の10進数からN進数への変換についても見ていきます。
変換の手順は以下のとおりです。
方法1:掛け算を使う
①小数部をN倍していく作業を、小数部が0になるまで続ける
②N倍した結果得られた整数部の値を順に並べる
方法2:重み表を使う
①N進法の重みを計算した重み表を作る
②引くことができる一番大きい重みを引いていく
方法1:掛け算を使う
例として方法1の手順で、10進数の「0.125」を2進数に変換してみます。
①小数部をN倍していく作業を、小数部が0になるまで続ける
小数部に、変換したい数の基数(今回は2進数への変換なので2)を掛けていきます。今回は、0.125を2倍していく作業を3回繰り返したところで、小数部が0になりました。
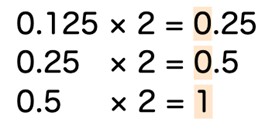
N倍する作業を繰り返すとき、小数部のみ取り出して掛けていくようにしてください。例えば10進数の「0.6875」を2進数に変換する場合、以下の手順となります。
0.6875 × 2 = 1.375
0.375 × 2 = 0.75
0.75 × 2 = 1.5
0.5 × 2 = 1
②N倍した結果得られた整数部の値を順に並べる
整数部の値を上から(計算結果を得た)順番に並べて、小数部の値とします。今回は変換前の値は整数部が0でしたので、変換後もそのまま0となり、10進数「0.125」の2進数への変換結果は「0.001」、10進数「0.6875」の2進数への変換結果は「0.1011」となります。
2進数以外のN進数の小数でも、同じ手順で変換できます。10進数の「0.125」を8進数に変換する場合は以下のようになります。
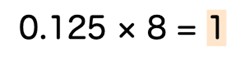
0.125を8倍すると、1回で小数部が0になりましたので、変換結果は「0.1」です。
それでは16進数の場合はどうなるでしょうか。
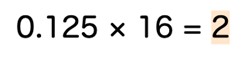
この場合の変換結果は「0.2」となります。
数値によっては、小数部が0にならない場合があります。例えば10進数の「0.6」を8進数に変換しようとすると、0.46314631463146314…と4631が繰り返されます。
このように小数部が無限に続く数のことを「無限小数」と呼び、今回の例のように同じ数字が繰り返される無限小数を「循環小数」と呼びます。
コンピューターで取り扱うことのできる桁数には限りがあるため、演算結果が無限小数となった場合は、最も近い値(近似値)を利用しています。
※近似値は実行環境(コンピュータのOS)や、使用しているプログラミング言語などにより異なります。
方法2:重み表を使う
次に方法2の手順で、10進法の「0.6875」を2進法の数に変換してみましょう。
①N進法の重みを計算した重み表を作る
2進法で重みを計算した表を作ります。
| 重み | 20 | 2-1 | 2-2 | 2-3 | 2-4 |
|---|---|---|---|---|---|
| 計算した重み | 1 | 0.5 | 0.25 | 0.125 | 0.0625 |
| 2進法の数 |
②引くことができる一番大きい重みを引いていく
②-① 0.6875 < 1 なので、0.5の重みの欄に 0.5 × □ <= 0.6875 となる「1」を書く。
| 重み | 20 | 2-1 | 2-2 | 2-3 | 2-4 |
|---|---|---|---|---|---|
| 計算した重み | 1 | 0.5 | 0.25 | 0.125 | 0.0625 |
| 2進法の数 | 1 |
②-② 残りは0.6875 – 0.5 = 0.1875。0.1875 < 0.25 なので、0.25の重みの欄には「0」を書く。
次に大きい0.125の重みの欄に 0.125 × □ <= 0.1875 となる「1」を書く。
| 重み | 20 | 2-1 | 2-2 | 2-3 | 2-4 |
|---|---|---|---|---|---|
| 計算した重み | 1 | 0.5 | 0.25 | 0.125 | 0.0625 |
| 2進法の数 | 1 | 0 | 1 |
②-③ 残りは0.1875 – 0.125 = 0.0625。0.0625の欄に「1」を書く。
| 重み | 20 | 2-1 | 2-2 | 2-3 | 2-4 |
|---|---|---|---|---|---|
| 計算した重み | 1 | 0.5 | 0.25 | 0.125 | 0.0625 |
| 2進法の数 | 1 | 0 | 1 | 1 |
これで小数部の値が求められました。変換結果は方法1と同じ「0.1011」です。
2進法以外のN進法
情報処理試験においては、8進法や16進法などもよく出題されますが、基本的な考え方は2進法と同じで、それぞれに基数の違いがあるだけです。
N進法の基礎をしっかりと理解して、応用が利くように準備しておきましょう。
N進数
○8進法
基本的なルールは以下のとおりです。
- 0〜7までの8種類の数字を使用する
- 数を数えるときは1桁に 0,1,2,3… と順番に入れていき、各桁が8になると桁がひとつ繰り上がる
- 各桁の重みは8のN乗(80、81、82、83…)
○16進法
基本的なルールは以下のとおりです。
- 0〜9,A,B,C,D,E,Fの16種類の英数字を使用する
- 数を数えるときは1桁に 0,1,2,3… と順番に入れていき、各桁が16になると桁がひとつ繰り上がる
- 各桁の重みは16のN乗(161、162、163、164…)
16進法では、10進法の10〜15をA〜Fに置き換えて表現することに注意してください。
| 10進法 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16進法 | A | B | C | D | E | F |
2進数と8進数、16進数同士の変換
基数が2のべき乗の数(2進数・8進数・16進数など)同士の変換は、比較的容易です。変換が容易な理由として、基数が2のべき乗である8進数や16進数は、本質的には2進数と言えるからです。例えば2進数4桁では0〜15までの数を表現できるので、複雑な計算をせず機械的に16進数1桁へ変換することができます。
変換の手順は以下のとおりです。
①変換する数を一定の桁ごとに区切る
②区切った単位で、基数変換を行なう
④②の結果をくっつける
・2進数から16進数への変換
例として、2進数の「1011111001」を16進数、8進数に変換してみましょう。
①変換する数を一定の桁ごとに区切る
区切る桁数は「変換する数の1桁が2進数の何桁で表現できるか」によって決まります。8進数であれば、1桁の最大値は8 = 最大23 = 3桁。16進数であれば、1桁の最大値は16 = 最大24 = 4桁で区切ります。
※桁が足りないところは0で補うようにしてください。
0010 | 1111 | 1001
②区切った単位で、基数変換を行なう(それぞれ1桁のN進数に変換される)
①で4桁ずつに区切った2進数を、それぞれ16進数に変換します(2進数を10進数に変換後、10進数を16進数へ変換します)。
0010 →0 × 23 + 0 × 22 + 0 × 21 + 0 × 20 =2(10進数の2は16進数の2)
1111 →1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 =F(10進数の15は16進数のF)
1001 →1 × 23 + 0 × 22 + 0 × 21 + 1 × 20 =9(10進数の15は16進数の9)
③②の結果をくっつける
上の桁から順番に並べて「2F9」という結果になります。
・2進数から8進数への変換
①変換する数を一定の桁ごとに区切る
8進数への変換ですので、「1011111001」を3桁で区切ります。3桁にするため先頭に「00」を加えます。
001 | 011 | 111 | 001
②区切った単位で、基数変換を行なう(それぞれ1桁のN進数に変換される)
①で3桁ずつに区切った2進数を、それぞれ8進数に変換します。
001 →0 × 22 + 0 × 21 + 1 × 20 =1(10進数の1は8進数の1)
011 →0 × 22 + 1 × 21 + 1 × 20 =3(10進数の3は8進数の3)
111 →1 × 22 + 1 × 21 + 1 × 20 =7(10進数の7は8進数の7)
001 →0 × 22 + 0 × 21 + 1 × 20 =1(10進数の1は8進数の1)
③②の結果をくっつける
上の桁から順番に並べて「1371」という結果になります。
・8進数から2進数への変換
同じ手順で、8進数の「1372」を2進数へ変換してみましょう。
①変換する数を一定の桁ごとに区切る
①N進数から2進数への変換の場合、N進数1桁を、2を基数とした場合のべき乗の桁数に変換していきます。今回は8進数からの変換ですので、8 = 23 = 3桁ずつに変換します。
1 | 3 | 7 | 2
②区切った単位で、基数変換を行なう
8進数の「1」・・・2進数の「001」
8進数の「3」・・・2進数の「011」
8進数の「7」・・・2進数の「111」
8進数の「2」・・・2進数の「010」
③②の結果をくっつける
上の桁から順番に並べて「1011111010」(先頭の0は無視)という結果になります。
・16進数から2進数への変換
同じように16進数の「1CB」を2進数へ変換してみます。
16進数からの変換ですので、16 = 24 = 4桁ずつに変換します。
1 | C | B
| 16進数の「1」 | 2進数の「0001」(16進数の1は10進数の1。よって2進数の「0001」) |
| 16進数の「C」 | 2進数の「1100」(16進数のCは10進数の12。よって2進数の「1100」) |
| 16進数の「B」 | 2進数の「1011」(16進数のCは10進数の11。よって2進数の「1011」) |
上の桁から順番に並べて「111001011」(先頭の0は無視)という結果になります。
ここまで整数について説明しましたが、小数の場合も手順は同じです。
・小数点ある16進数から2進数への変換
16進数の「0.9A26」を2進数に変換してみましょう。
①変換する数を一定の桁ごとに区切る
②区切った単位で、基数変換を行なう
16進数からの変換ですので、小数部の各桁を 16 = 24 = 4桁ずつの2進数に変換します。
9・・・1001
A・・・1010
2・・・0010
6・・・0110
③②の結果をくっつける(末尾の0は無視)
0.100110100010011
8進法や16進法は、基数が2のべき乗であることから2進法との相性が良く、コンピューターにとっては処理しやすい数です。現在、コンピューター内部で主に使用されているのは2進法と16進法ですが、8進法も一部使用されているケースがあります。
2進数、8進数、16進数、10進数以外の基数変換
ここまで10進数とN進数の基数変換について説明してきましたが、例えば3進数と7進数などの基数変換は、どのように行なえば良いでしょうか。
M進数からN進数(M,N=2,8,16,10以外)へ変換する手順は以下のとおりです。
①M進数を10進数に変換する(M進数→10進数)
②①の10進数をN進数に変換する(10進数→N進数)
計算のステップはひとつ増えてしまいますが、一度10進数へ変換した後で、求めたい基数に変換します。
例として3進数の2120を7進数に変換してみましょう。
①M進数を10進数に変換する(M進数→10進数)
3進数の2120を10進数に変換します。手順は前述の「○整数部のN進数から10進数への変換」を参照してください。
変換結果は「69」となります。
②①の10進数をN進数に変換する(10進数→N進数)
10進数の69を7進数に変換します。手順は前述の「○整数部の10進数からN進数への変換」を参照してください。
変換結果は「126」となります。
情報処理試験においては、2進数・8進数・16進数と10進数の変換が多く出題されますが、それ以外の基数変換についても覚えておいて損はありません。
演習問題にチャレンジ!
それでは最後に、本記事で学習した内容への理解を深めるため、演習問題に挑戦してみましょう。演習問題は全部で4問あります。
【問題1】2進数から10進数への変換
2進数の110011011を10進数に変換してください。
【解答と解説】
解答:411
N進法の数から10進法の数への変換手順は以下のとおりです。
———————————————————
①N進法の数の各桁の値に、その桁の「重み」を掛ける
②各桁の1.の結果を足し算する
———————————————————
問題1の数を手順に沿って変換していきます。
110011011
= (1×28) + (1×27) + (0×26) + (0×25) + (1×24) + (1×23) + (0×22) + (1×21) + (1×20)
= 256 + 128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 = 411
【問題2】10進数から2進数への変換
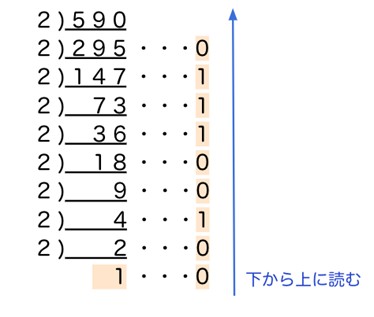
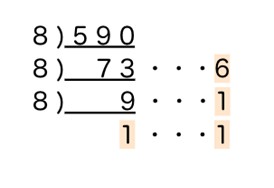
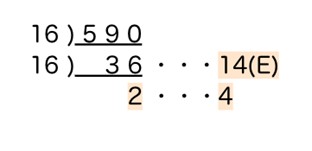
10進数の590を2進数・8進数・16進数に変換してください。
【解答と解説】
解答:2進数「1001001110」、8進数「1116」、16進数「24E」
10進法の数からN進法への変換手順は以下のとおりです。(本記事の方法1の場合)
———————————————————
①10進法の数をNで割っていき、余り(0または1)を計算する
②①の結果を下から上に順に並べていく
———————————————————
問題2の数を手順に沿って変換していきます。
2進数への変換は以下のように行ないます。
8進法数への変換は以下のように行ないます。
16進数への変換は以下のように行ないます。
【問題3】小数点以下の基数変換
10進数の演算式 5÷32 の結果を2進数で表してください。
【解答と解説】
解答:0.00101
5÷32の計算結果は0.15625です。0.15625を2進数で表すには、小数部が0になるまで2倍していき、最後に計算結果を並べます。
0.15625 × 2 = 0.3125
0.3125 × 2 = 0.625
0.625 × 2 = 1.25
0.25 × 2 = 0.5
0.5 × 2 = 1
【問題4】N進数同士の変換
以下の表は、同じ値を2進数・8進数・10進数・16進数で表しています。空欄を埋めて表を完成させましょう。
| 2進数 | 8進数 | 10進数 | 16進数 |
|---|---|---|---|
| 15 | |||
| 63 | |||
| 8C | |||
| 1011101.01 |
【解答と解説】
表をすべて埋めると以下の結果になります。
| 2進数 | 8進数 | 10進数 | 16進数 |
|---|---|---|---|
| 1101 | 15 | 13 | D |
| 111111 | 77 | 63 | 3F |
| 10001100 | 214 | 140 | 8C |
| 1011101.01 | 135.2 | 93.25 | 5d.4 |
